I. Course essential information
Course code | B07M3030 |
Course Name | Probability Theory and Statistics and Stochastic Process |
Credits/Periods | 3.5 credits / 64 periods |
Period Allocation | Lecture: 64;others: 0 |
Course Classification | Basic course |
Semester | Second semester |
Faculty | College of Mathematics |
Major Program | Majors in science and engineering |
Language of Instruction | English |
Prerequisites | Advanced mathematics |
Follow up Course | None |
Course Introduction | The course introduces random events and their probabilities, probability distributions and numerical characteristics of random variables, law of large numbers, central limit theorem, parameter estimation and hypothesis testing. Students will enhance abilities in data analysis and modeling. |
II. Course content and Time allocation
1. Random events and probabilities (8 periods/in class)
1) Random experiments, sample spaces, random events and relationships between random events.
2) Probabilities, conditional probabilities, classical probability models, geometric probability models, and probability calculation in random events.
3) Formulas of probability, Bayes formula and their applications.
4) Independence of random experiments, Bernoulli experiment, and probability calculation.
2. Random variables and probability distributions (7 periods/in class)
1) Random variables, distribution function of random variables, distribution law of discrete random variables, probability density of continuous random variables.
2) Probability calculation of events by probability distribution of random variables, calculation of probability density or distribution function.
3) Typical random variables and their probability distribution, including 0-1 distribution, binomial distribution, Poisson distribution, geometric distribution, Negative binomial distribution, uniform distribution, exponential distribution and normal distribution.
4) Poisson theorem, and approximation of binomial distribution by Poisson distribution.
5) Probability distribution calculation of random variable functions by probability distribution of independent variables, including linear functions, power functions, exponential functions, logarithmic functions and Trigonometric functions.
3. Random vectors and probability distributions (8 periods/in class)
1) Two-dimensional random vectors, joint probability distribution functions, joint distribution density functions and law of joint distribution.
2) Marginal distribution function, marginal distribution density and law of marginal distribution.
3) Independence of random variables and judgment.
4) Two-dimensional uniform distribution, two-dimensional normal distribution, and key parameters in two-dimensional normal distribution.
5) Probability distribution of random vector functions.
4. Numerical characteristics of random variables (7 periods/in class)
1) Expectations, variances, standard deviations, moments, covariances, correlation coefficients.
2) Numerical characteristics of common distributions, including 0-1 distribution, binomial distribution, Poisson distribution, uniform distribution, exponential distribution and normal distribution.
3) Calculation of numerical characteristics by definition and properties, and expectation calculation of random variable function 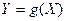 or random vector function
or random vector function 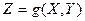 .
.
4) Correlation and independence, especially relationship between uncorrelation and independence.
5. Law of large numbers and central limit theorem (3 periods/in class)
1) Convergence in probability for random variable sequences.
2) Chebyshev’s inequality, Chebyshev’s theorem of large numbers, Khinchine’s theorem of large numbers, Bernoulli’s theorem of large numbers.
3) Central limit theorem for random variable sequences, Levy-Lindberg’s theorem and DeMoivre-Laplace’s theorem.
6. Basic concepts of mathematical statistics (4 periods/in class)
1) Universes, simple random samples, sample means, sample variances and sample moments.
2) 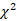 -distribution, t-distribution, F-distribution, and calculation by tables.
-distribution, t-distribution, F-distribution, and calculation by tables.
3) Distribution of a statistic in a normal population
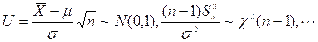 .
.
7. Parameter estimations (7 periods/in class)
1) Point estimation, estimator, estimation value, moment estimation method and maximum likelihood estimation method.
2) Unbiasedness, effectiveness, consistency and method to examine.
3) Interval estimation and confidence intervals.
8. Hypothesis testing (5 periods/in class)
1) Basic concepts and steps of hypothesis testing.
2) Mean and variance hypothesis testing for normal populations and bivariate normal populations.
3) Two kinds of mistake in hypothesis testing.
4) Person fitting test.
9. Basic concepts of Stochastic process (7 periods/in class)
1) Stochastic processes, families of finite-dimensional distributions, mean functions, variance functions, autocorrelation functions and autocovariance function.
2) Calculation of mean functions, variance functions, etc.
3) Homogeneous independent increment processes, Poisson processes and Wiener processes.
10. Markov chain (8 periods/in class)
1) Markov processes, Markov chain, transition probabilities and transition probability matrices.
2) Calculation of transition probability matrices and Chapman-Kolmogorov equations.
3) One-dimensional and n-dimensional distribution calculation of homogeneous Markov chains.
4) Ergodicity of homogeneous Markov chains and stationary distribution calculation of homogeneous Markov chains.